Nevsk. Истоки современной математики начинаются в древней Индии

Математика (др.-греч. изучение, наука) занимается операциями с числами, описаниями и измерениями формы объектов. Она не относится к наукам естественным – математические объекты создаются хоть и на основе свойств реальных объектов, но в идеальном, абстрактном виде, а запись их свойств производится в виде формул на формальном языке.

И все-таки математика — фундаментальная наука, предоставляющая средства всем другим наукам и помогает им описать изучаемые предметы, выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы. Другими словами можно сказать, что в то время как естественные науки имеют дело с миром вещественным, математика оперирует идеями. Еще древнегреческий мудрец Пифагор в VI в. до н.э. учил, что Вселенная создана Числом.

Кстати, Учение о Числах «величайшего эллинского мудреца» Пифагора не было его собственным изобретением, он перенял его в своих странствиях по Востоку – Египту, Халдеи, Индии. Именно там кроются его науки о числах. Также и кабалистическая Книга Творения «Сефер Иецира», в которой сфироты – это ничто иное как числа, была списана евреями с халдейской «Книги Чисел», а халдеи, в свою очередь, наследовали это знание от древних индийцев.

Арифметика изучает действия над числами (в основном над положительными рациональными).

Алгебра, в отличие от арифметики, изучает общие методы решения задач при помощи уравнений. Для этого в алгебре используются буквенные обозначения.

Геометрия исследует пространственные объекты (точки, прямые, кривые, плоскости, поверхности, векторы) и отношения между ними.

Математический анализ изучает функции.

В комплексном анализе тоже рассматриваются функции, но они зависят от комплексного аргумента.

Функциональный анализ изучает бесконечномерные пространства. Он использует методы алгебры, геометрии, математического анализа и других разделов. Благодаря этому функциональный анализ помогает установить связи между различными разделами математики.

Математическая логика – это раздел математики, посвященный математическим доказательствам.

Численные методы посвящены приближенному решению математических задач. На численных методах базируются вычисления на ЭВМ.

Теория вероятностей – это раздел математики, который изучает случайные события, т.е. события, которые могут произойти, а могут и не произойти.

Развитие математики как науки в каждой древней цивилизации начиналось со счета. Он был неотъемлемой частью эволюции всего человечества. С помощью математического счета человек вел хозяйство, контролировал поголовье скота, производил расчет календаря, вел торговлю и т.п. Параллельно социуму развивалась и математика, которая начала свое движение со счета.

Принято считать, что основы математики заложили древние греки или вавилоняне. Однако основоположниками арифметики и алгебры оказались древнеиндийские ученые, которые пошли дальше греков и вавилонян. Величайшим достижением древнеиндийской математики является, прежде всего, открытие позиционной системы счисления, состоящей из десяти индийских цифр, включая и знак нуль (подробнее см. Рампрасад Согал. История арабских (индийских) цифр. Ноль и десятичная система счисления).

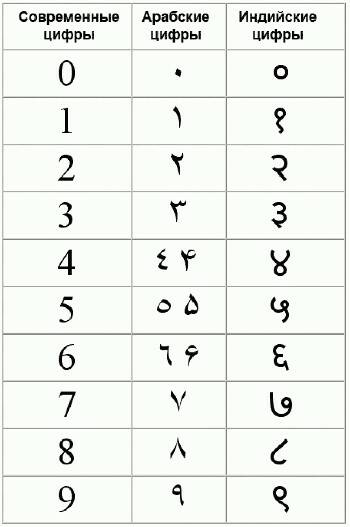
Индийские арабские цифры

Они изобрели привычную нам десятичную позиционную систему записи чисел, предложили символы для 10 цифр (которые, с некоторыми изменениями, используются повсеместно в наши дни), систематическое употребление нуля для обозначения отсутствия единиц данного разряда, а также заложили основы десятичной арифметики, комбинаторики, разнообразных численных методов, в том числе тригонометрических расчётов.

Арабские цифры являются всего лишь видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму. Один из крупнейших ученых средневековья, арабский математик и астроном Аль-Хорезми , автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра», широко популяризировал индийскую систему записи.

Абу Джафар Мухаммад ибн Муса ал-Хорезми (783–850),(783–850), среднеазиатский математик, астроном, историк, географ.

Он написал книгу «Об индийском счёте», способствовавшую распространению десятичной позиционной системы записи чисел во всём Халифате, вплоть до Мусульманской Испании.

Ещё недавно европейские математики указывали на древнегреческого астронома, механика и математика Гиппарха Никейского (190 – ок. 120 до н. э.) как на отца тригонометрии, хотя всё, что они когда-либо могли узнать о нём, почерпнуто со слов его же ученика Птолемея. В Индии была найдена древняя рукопись, доказывающая, что «уравнение центра» было известно индусам задолго до Р.Х.

Раскопки в Хараппе, Мохенджо-Даро и других поселениях Цивилизация долины Инда возрастом около 5000 лет обнаружили свидетельства использования «практической математики». Древние индийцы производили кирпичи, размеры которых составляли 4: 2: 1, что считалось благоприятным для устойчивости кирпичной конструкции. Они использовали стандартизированную систему весов: 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200 и 500, с единицей измерения веса, равного примерно 28 граммам (примерно греческой или английской унции). Массово производились грузы правильной геометрической формы, включая шестигранники, конусы и цилиндры, демонстрируя тем самым знание основ геометрии.

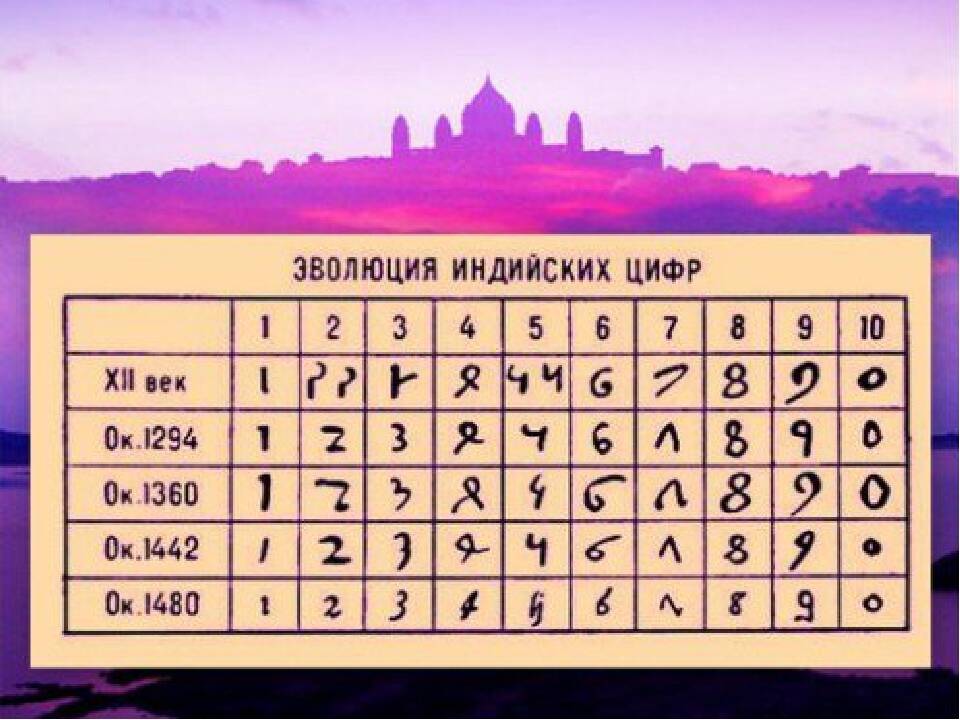
Эволюция индийских (арабских) цифр https://www.letopis.info/

Жители цивилизации Инда также пытались стандартизировать измерение с высокой степенью точности. Они разработали линейку Мохенджо-даро, единица длины которой (1,32 дюйма или 3,4 см) была разделена на десять частей.

Полые цилиндрические предметы, сделанные из ракушек и найденные в Лотхале (2200 г. до н.э.) и Дхолавире (это древние города Хараппской цивилизации), показали способность древних индийцев измерять углы в плоскости, а также определять положение звезд для навигации.

Математика в древней Индии https://travel-in-time.org/

Кстати, математика древней Индии была тесно связана с религией. В геометрическом сборнике «Шульба-сутры» (дополнение к Ведам, тексты, относящиеся к ведическим ритуалам, датируются VIII – V веками до н.э.) описывается построение жертвенных алтарей, математические правила перемежаются с ритуальными предписаниями. В «Шульба-сутрах» есть задачи на построение квадратов и прямоугольников, частные случаи теоремы Пифагора. Из этих задач видно, что индийцы знали дроби, умели извлекать квадратные корни, пользовались точными и приближенными методами для нахождения площадей и объемов.

Индийские математики далекого прошлого также любили состязаться на публичных народных собраниях. По этому поводу один индийский автор VII века, заканчивая свою книгу, писал: «Подобно тому, как солнце затмевает своим блеском звезды, так мудрец затмевает славу других людей, предлагая и особенно решая на народных собраниях математические задачи».

Еще в глубокой древности Индия славилась знаниями в области грамматики, математики, астрономии и других наук. Народы Индии уже тогда создали богатую и своеобразную культуру. Кстати, самый первый университет в мире был основан в Индии в VII веке (раскопки показывают руины постройки Х века до н.э.) в в городе Таксила на территории современного Пакистана, у подножия Гималаев и Памира. Более 10,5 тыс. студентов со всех концов света (Сирии, Вавилонии, Греции, Китая) изучали более 60 предметов, а также из .Буддистский университет Наланда, построенный в Индии начале V века (на территории современного индийского штата Бихар) –древний центр высшего образования с 427 по 1197 год. одно из самых выдающихся достижений древней Индии в сфере образования.

Развалины древнего университета Наланда. Древнейший в мире буддийский университет и монастырский комплекс, существовавший в V—XII веках на севере Индии, один из крупнейших образовательных центров своего времени,в котором работали, преподавали и обучались многие выдающиеся буддийские философы из разных стран, и куда съезжались многочисленные паломники. Раскопанная археологическая зона занимает площадь около 150,000 м², но ещё значительная часть раскопок не произведена. В расположенном поблизости музее хранятся манускрипты, обнаруженные при раскопках http://dostoyanieplaneti.ru/

Катьяяна (с VI по III век до н.э.) был ведическим математиком и священником, жившим в древней Индии. Он примечателен тем, что написал одну из поздних книг Шульба-Сутр, в которой была представлена геометрия конструкций ведических алтарей (прямоугольников, прямоугольных треугольников, ромбов), включая общую теорему Пифагора и вычисление квадратного корня из 2 с точностью до пяти десятичных знаков.

Джайнская математика (400 г. до н.э. – 200 г. н.э.) внесла значительный исторический вклад тем, что джайнские математики освободили индийскую математику от религиозных и ритуальных ограничений. Например, их тексты определяют пять различных типов бесконечности: бесконечное в одном направлении, бесконечное в двух направлениях, бесконечное по площади, бесконечное везде и бесконечное вечно. Кроме того, джайнские математики разработали обозначения для простых степеней (и показателей) чисел, таких как квадраты и кубы, что им определяют простые алгебраические уравнения.

Интересные факты возвращают нас к алгебре в Индии. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.). Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: притом предполагалось, что в нём все коэффициенты, кроме a, могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным. Индийская арифметика была известна в средневековой Европе как modus Indorum, что означает “метод индийцев”.

Наибольшие числа, которыми оперировали греки и римляне, составляли числа 10⁶ , то есть миллион, тогда как индийские ученные использовали числа порядка 10⁵³ (10 в степени 53). Числа таких порядков имели свои собственные названия в Индии. Даже в наши дни наибольшее число с собственным названием – Терра 10¹² (10 в степени 12). Также в Индии была изобретена самая большая единица времени, кальпа — время от рождения вселенной до её полного уничтожения. Прием, она с точностью до 5 % совпадает с предположительным возрастом Земли (4,54—4,57 млрд лет). В «Книге рекордов Гиннесса» кальпа числится как самая большая единица измерения времени.

В истории Индии имеется много фактов, свидетельствующих об экономических и политических связях с византийским и арабским миром и с Китаем. В математике считается бесспорным индийское происхождение десятичной системы счисления с нулем и правил счета. Кроме того, индийцы достигли небывалого успеха в алгебре. Их символика значительно богаче, нежели у Диофанта.

Диофант Александрийский – древнегреческий математик

Диофант Александрийский — древнегреческий математик, живший предположительно в III веке н. э. Нередко упоминается как «отец алгебры». Автор «Арифметики» — книги, посвящённой нахождению положительных рациональных решений неопределённых уравнений. В наше время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел.

Диофант был первым греческим математиком, который рассматривал дроби наравне с другими числами. Диофант также первым среди античных учёных предложил развитую математическую символику, которая позволяла формулировать полученные им результаты в достаточно компактном виде.

Древние индийцы придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры.

Так, в одной старинной русской рукописи описывается интересный прием «умножения крестиком», применявшийся еще в древней Индии под названием «молниеносного».

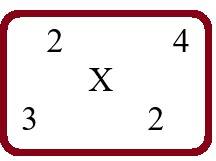
Умножение крестиком

Пример:  24 х 32 = 768  Последовательно производим следующие действия: 1). 4 х 2 = 8 – это последняя цифра результата, 2). 2 х 2 = 4;  4 х 3 = 12; 4 + 12 = 16. 6 – предпоследняя цифра в ответе, единицу запоминаем. 3). 2 х 3 = 6,  6 + 1 = 7 – это первая цифра в ответе. Ответ – 768. Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.

Древнеиндийские ученые также внесли большой вклад и в тригонометрию. Так, освещая свойства треугольников и их использование при решении задач астрономии, Птолемей рассматривал величину хорды дуги окружности (эквивалент удвоенного синуса половины центрального угла, стягивающего дугу). Выражения хорд некоторых дуг через радиус окружности легко находятся как стороны соответствующих вписанных в неё правильных многоугольников (треугольника, квадрата, шестиугольника и других, что для хорд дуг в 120°, 90°, 60° и других даёт R√3/2, R√2/2, R/2 и т.д.).

Птолемей составил довольно точную таблицу хорд дуг от 0 до 180° через 1° равнозначную таблице синусов углов от 0 до 90° через ½°.

Учёные Индии вместо хорды дуги — «тетивы лука» стали рассматривать её половину, которая в результате не совсем точных переводов получила название синус, а также две другие тригонометрические величины, названные в дальнейшем косинусом (синус угла, дополняющий рассматриваемый до 90°) и синусом-верзусом (дополнение косинуса до радиуса окружности).

В V веке индийцы располагали таблицей синусов от 0 до 90° через 3¾°. Для определения высот и расстояний, а затем и решения астрономических задач они пользовались тенью вертикального шеста — гномона.

Индийский математик, астроном и астролог Варахамихира 505—587) заменил хорду (дживу) половиной хорды. В его «Панча-сиддханте» использовались понятия котиджива и уткра-маджива. Все эти понятия в VIII веке заимствовали арабские математики; термин джива они изменили на джиба, а затем и на джайб – впадина, изгиб, излучина. Этот термин был переведен с арабского языка на латинский в его буквальном значении словом sinus. Cosinus – сокращение от complementisinus (дополнение синуса).

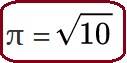В «Панча-сиддханте» Варахамихира пользуется некоторыми интересными математическими результатами; принадлежат ли они ему самому или он ими пользуется по традиции, сказать с определённостью невозможно. Для вычисления площади круга Варахамихира пользуется приближением π = квадратный корень из 10. Здесь же приводится основное тригонометрическое тождество и ряд других соотношений плоской тригонометрии.

Научные достижения индийской математики широки и многообразны. Расцвет индийской математики относится к V–XII вв. Наиболее известные индийские математики:

Ариабхата (476—550) — индийский астроном и математик. Его деятельность открывает «золотой век» индийской математики и астрономии. Он описывает процесс извлечения квадратного и кубического корня в десятичной системе счисления; даёт формулы для площади круга и объёма сферы; а также приводит приближённое значение для числа пи (π) — отношения длины окружности к её диаметру ((4 + 100) × 8 + 62000)/20000 = 62832/20000 = 3,1416), встречающееся ранее в «Пулиса-сиддханте» и приведённое затем (после перевода трудов Ариабхаты на арабский) Аль-Хорезми (783-850). В своём сочинении Ариабхата приводит весьма точные данные для размеров Земли и Луны.

Кстати, Аль-Хорезми является автором серьёзных трудов по астрономии. В них он рассказывает о календарях, расчётах истинного положения планет, расчётах параллакса и затмения, составлении астрономических таблиц (зидж), определении видимости луны и т. д. В основу его работ по астрономии легли труды индийских астрономов.

Брахмагупта (ок. 598 — 670) — индийский математик и астроном. Руководил обсерваторией в Удджайне. Оказал существенное влияние на развитие астрономии в Византии и исламских странах, стал использовать алгебраические методы для астрономических вычислений, ввёл правила операций с нулём, положительными и отрицательными величинами. Брахмагупта, как и Ариабхата, систематически применял непрерывные дроби, теория которых отсутствовала у греков.

Шридхара Ачарья (ок. 870 – ок. 930), он отделил алгебру от арифметики и был первым, кто дал формулу для решения квадратных уравнений, 

Бхаскара I (ок. 600 – ок. 680) – выдающийся индийский математик и астроном. В 1979 году Индийская организация космических исследований запустила космичесский спутник “Bhaskara I” в честь математика.

Бхаскара II (1114—1185) — крупнейший индийский математик и астроном XII века. Он возглавлял астрономическую обсерваторию в Удджайне. Ему принадлежат целочисленные решения линейных и квадратных неопределенных уравнений ( Куттака ). Правила, которые он дает, фактически такие же, как те, что были даны европейскими математиками эпохи Возрождения XVIII века. Также он вывел циклический метод Чакравала для решения неопределенных уравнений вида ax ² + bx + c = y . Решение этого уравнения традиционно приписывалось Уильяму Броункеру в 1657 году, хотя его метод был сложнее, чем метод Чакравала.

Работа Бхаскара по исчислению предшествовала Ньютону и Лейбницу более чем на 500 лет. Он особенно известен открытием принципов дифференциального исчисления и его применения к астрономическим задачам и вычислениям. Хотя Ньютону и Лейбницу приписывают дифференциальное и интегральное исчисление, есть убедительные доказательства того, что Бхаскара был пионером в некоторых принципах дифференциального исчисления.

Он разработал сферическую тригонометрию вместе с рядом других тригонометрических решений. Возможно, он был первым, кто придумал дифференциальный коэффициент и дифференциальное исчисление.

Древнеиндийская логарифмическая шкала времени в секундах

Более того, Ему принадлежит один из самых ранних проектов вечного двигателя. Самое раннее упоминание о вечном двигателе относится к 1150 году, когда Бхаскара II описал колесо , которое, как он утверждал, будет работать вечно.

Бхаскара был знаком с концепцией бесконечно малых чисел. Так, при вычислении мгновенного движения планеты временной интервал между последовательными положениями планет не превышал трути (truti) , или 1/33750 секунды , и его мера скорости выражалась в этой бесконечно малой единице времени.

Бхаскара точно определил многие астрономические величины, включая, например, продолжительность звездного года , время, необходимое Земле для обращения вокруг Солнца, как примерно 365,2588 дней, что составляет то же, что и в ведическом тексте Сурья-сиддханта. Современное принятое измерение составляет 365,25636 дней, разница в 3,5 минуты!

Южноиндийский математик Мадхава из Сангамаграмы (1340–1425) и математики школы Кералы (включая Парамешвару) с XIV по XVI века расширили работs Бхаскары и продвинули развитие математики в Индии.

Он был первым, кто использовал приближения бесконечных рядов для ряда тригонометрических функций, что было названо решающим шагом вперед от конечных процедур древней математики к рассмотрению их предельного перехода к бесконечности. Многие работа Мадхавы и других математиков школы Кералы была передана в Европу через иезуитских миссионеров и торговцев, которые в то время активно действовали в Южной Индии, что повлияло на более поздние европейские разработки в области математического анализа и исчисления,

К сожалению, математические и астрономические труды индийцев, написанные в XV–XVII вв., и в частности такое замечательное открытие, как бесконечные ряды для арктангенса, синуса и косинуса, остались в свое время неизвестными за пределами Индии и были получены вновь европейцами. Привычные нам термины «корень» и «синус» постоянно напоминают нам о роли индийских ученых, особенно южноиндийких, в разработке алгебры и тригонометрии.

Южноиндийские ученые предвосхитили многие результаты, которые были вновь получены в Европе в XVII — XVIII вв. Так, ряд арктангенса был вновь найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г. Соотношением пользовался в 1739 г. Эйлер для разложения числа р. Ряды для синуса, косинуса и арксинуса были выведены И. Ньютоном около 1666 г.

Кстати, по поводу бинома Ньютона классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается в сутрах, начиная примерно с IV в. до н.э. Индийские математики первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона. Во II в. до н.э. индийцы уже знали, что сумма всех биномиальных коэффициентов степени n равна 2ⁿ. Ньютон же вывел формулу бинома для более общего случая.

Двоично-десятичное кодирование

В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр, при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Двоично-десятичные числа требуют большего количества битов для своего хранения.

Таблица сложения в десятичной системе счисления.

Десятичная непозиционная система счисления с единичным кодированием десятичных цифр (от 1 до 1 000 000) возникла во второй половине III тыс. до н. э. в Древнем Египте (египетская система счисления). В другой великой цивилизации — вавилонской с её шестидесятеричной системой — за две тысячи лет до н. э. внутри шестидесятеричных разрядов использовалась позиционная десятичная система счисления с единичным кодированием десятичных цифр. Египетская десятичная система повлияла на аналогичную систему в первых европейских системах письма, таких как критские иероглифы, линейное письмо А и линейное письмо Б. Также в Древнем Риме использовалась непозиционная система счисления.

Древнейшая же известная запись позиционной десятичной системы обнаружена в Индии в 595 г.н.э.

См. еще:

Nevsk. Символика нуля. История цифры и числа “ноль”

Рампрасад Согал. История арабских (индийских) цифр. Ноль и десятичная система счисления

Ведантист. Сурья-сиддханта. Современные астрономические знания у древних индийцев

Элен. Теорема Пифагора. Кто её открыл?

Кэтрин. Родиной шахмат является Индия?

• Ключевые слова: математик,индийские математики,индийской математики,древних индийцев,тригонометри