Валерий Куликов. “Estrella” – чертеж Великой Пирамиды в горах Наска

В своей статье Д.Нечай, обратил внимание на “странности” геоглифа называемого на местном наречии “Estrella” (“Звезда”), обнаруженного не так давно в скалистых районах местечка Пальпа в Перу, пососедству с нашумевшим в прошлом столетии райном Наска, где обнаружены тысячи линий прямых и не очень, явно искусственного происхождения. А. Жуков, побывавший там в этом году, подвез новых аэрофотоснимков и новых впечатлений.

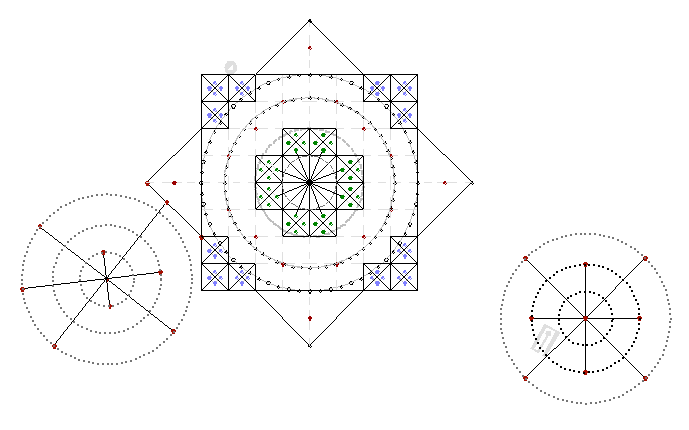
Геоглиф действительно необычный. Его отличает преобладание геометрических фигур, собранных в единую легко читаемую геометрическую композицию. Он располагается на относительно ровной площадке, порядка километра длиной, в скалистой местности, со сложным рельефом, с координатами 14°33’20” южной широты и 75°10’30” западной долготы.

Фотографии геоглифа я размещу в приложении, но смысл геометрии чертежа можно рассматривать и на схематическом рисунке, который достаточно точно, для уровня иллюстративной графики, показывает содержательную сторону. К тому же, сам геоглиф на такой уровень и рассчитан.

Прежде всего, анализ составных частей геоглифа показывает, что это не просто декоративный рисунок.

В композиции присутствуют закономерности, говорящие о том, что используемые в ней элементы носят информативный характер, и расположение их в рисунке подтверждает то, что они не случайны. Семантические признаки элементов говорят о содержательности и иллюстративности изображения, о том, что геоглиф предназначен именно для прочтения.

Кроме того, закономерности эти складываются в определенные правила, задающие логические направления, некоторые векторы, в направлении которых, согласно этим правилам, композиция может дальше развиваться. Способность к развитию системы, так же подтверждается в ходе анализа. Таким образом, она обладает динамическими свойствами, способностью к развитию. И инструкции к развитию находятся в самой же композиции.

Элементы композиции представляют собой структурные паттерны, со свойствами самой системы. А это говорит о том, что композиция обладает признаками структурной рекурсии.

В композиции демонстрируются свойства двух противоположных систем – ортогональной и радиальной. Обе эти системы взаимодействуют и одновременно влияют друг на друга, вызывая в системе внутренние напряжения и стремление к устранению конфликта. Структурные изменения происходящие при этом переводят всю композицию на другой уровень, и процесс повторяется снова.

Прямоугольная и радиальная система – две основных структурообразующих категории окружающего мира, и изображенные на 2-х мерном геоглифе общие законы взаимодействия пространственных ячеек легко проецируются на 3-х мерное пространство.

И тут обнаруживаются ориентиры, позволяющие применить четырехгранную пирамиду в качестве того самого геометрического тела, которое наиболее полно отображает процессы взаимодействия квантов пространства, находящихся в конфликтной ситуации полярной и прямоугольной системы. В дополнение к теоретическим связям, совпадение геометрии внутренней структуры Великой пирамиды с рисунком геоглифа, позволяет предположить, что эти два памятника связаны между собой если не на прямую, то, по крайней мере, являются разными стадиями идентичных процессов “проект – реализация”, что геоглиф является принципиальной схемой процессов происходящих на уровне квантов в деформируемом пространстве пирамиды. Может быть так именно и работает геометрия пи-пирамиды, удивляя нас чудесами дегидрации, изменением структуры и скорости роста кристаллов, заточенными лезвиями, повышением урожайности зерновых и пр.

Чертеж не имеет пояснительной записки или инструкции по эксплуатации, но тонко манипулирует ассоциативными понятиями, предоставляя возможность прочесть закономерности как символы, расположение которых, как в предложении, составляет единую смысловую конструкцию.

На отдельных страницах я попытаюсь объяснить эти, действительно удивительные, свойства, на первый взгляд простой, восьмиконечной звезды. Элементы в ней настолько взаимоувязаны, что возникающая сложность и многослойность внутренних взаимоотношений просто удивляет.

Выделим основные составляющие композиции:

1.Собственно сама восьмиконечная звезда, образуемая двумя квадратами: основной 8х8 и диагональный со стороной 12.
2.Замаркированные ячейки маркировочными квадратами и перекрестиями диагоналей.
3.Маркировочные точки. (или маркировочные квадраты, образуемые 4-мя точками, а в действительности круглыми ямями).
4.16-ти лучевая звезда в центре.
5.Концентрические окружности. Окружности делятся последовательным делением на 2. Большая заметно делится на 32 части большими точками, а затем каждый сегмент еще на двое точкой поменьше, итого – 64

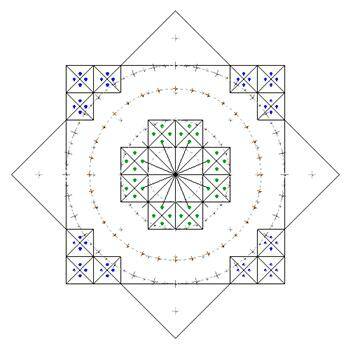
Рис. 1

Прежде всего, нужно заметить, что мы имеем восьмиконечную звезду, отличающуюся от “правильной” восьмиконечной звезды, тем что состоит она из разных по размеру квадратов, и это объясняется тем, что наша композиция строится по модульной прямоугольной сетке. Восьмиугольник, образуемый пересечением квадратов получается не равносторонний (Рис. 2.а).

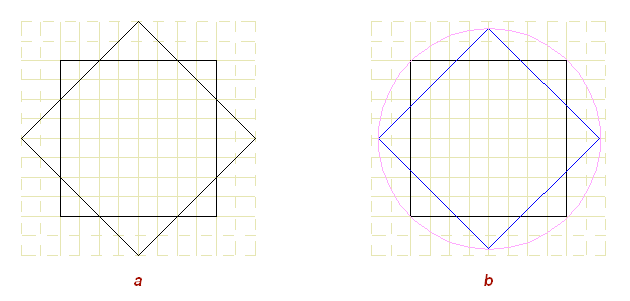
Рис. 2

В правильной звезде (Рис. 2.b), построенной разворотом двух равновеликих квадратов, все уравновешено: отсекаемые треугольники равны между собой, в результате остается совершенно правильный восьмиугольник, имеет 16 осей симметрии повернутые на одинаковый угол относительно друг друга (360/16). Эти свойства приближают правильную звезду к окружности.

Иными словами, она обладает свойствами полярной или радиальной системы, где равновеликие величины равноудалены от центра.

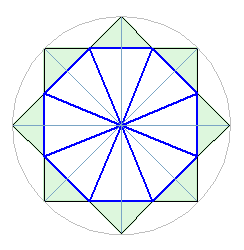
Рис. 3

Но есть один недостаток: правильная звезда не укладывается в модульную сетку. Длина стороны восьмиугольника, как и длины сторон треугольников получаются иррациональными числами, основанными на бесконечном в дробной части числе sqrt(2). (иными словами ее трудно нарисовать на листочке в клеточку).

Это свойство отдаляет ее от квадрата, который является прямым полномочным представителем ортогональной системы. В модульной прямоугольной системе равные величины располагаются параллельно осям (а не по окружности, как в полярных системах).

Квадрат и равносторонний треугольник – две правильные фигуры, которые способны делиться на себе подобные без остатка. Т.е. площадь этих фигур заполняется полностью подобными им фигурами кратными им по размеру. Что придает этим фигурам важное свойство – модульность, определяющее параметры их внутреннего пространства. Каждая составляющая такой системы может быть самостоятельной подобной системой.

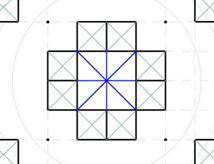
Рис. 4
Но вернемся к узорам.

Из центра композиции на геоглифе расходятся 16 лучей. Восемь направлений (ортогональные и диагональные) совпадают с модульной сеткой.

С остальными – проблема. Возможны два варианта:

a) подчиниться правилу ортогональной системы и разделить пополам сторону ячейки (вариант а, Рис. 5);

b) либо по правилу правильной звезды разделить пополам угол (вариант b, Рис. 5):

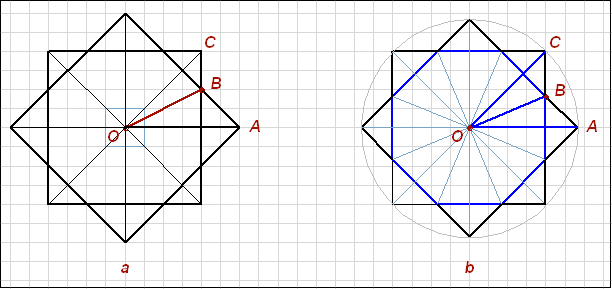
Рис. 5

В первом случае мы следуем правилу общей композиции, но сталкиваемся с ее недостатком: угол AOB не равен углу BOC.

Во втором случае, мы получаем 16 лучей равномерно распределенных по окружности, но теряем равномерное деление сторон квадрата.

(то же, но увеличим центральную часть)

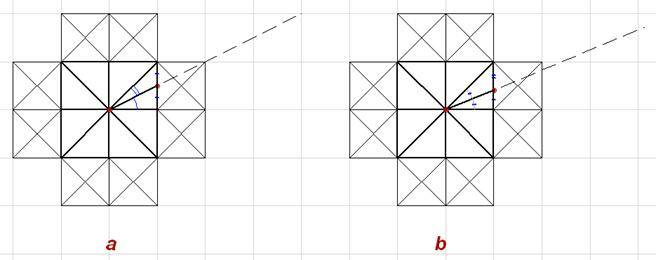
Рис. 6

При неточности скального рисунка (а там погрешности в этом масштабе около 1-2 толщины линии), было бы трудно отличить какой именно вариант там используется. Лучевая звезда в разных вариантах выглядела бы почти одинаково.

Но об этом позаботились. На геоглифе точки через которые проходит луч обозначили:

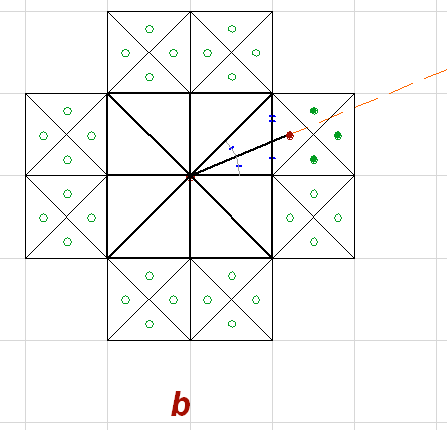
Рис. 7

Точка лежит на середине высоты ячейки, но сдвинута от вертикальной стороны.

Только в этой точке биссектриса угла пересечет горизонтальную ось ячейки.

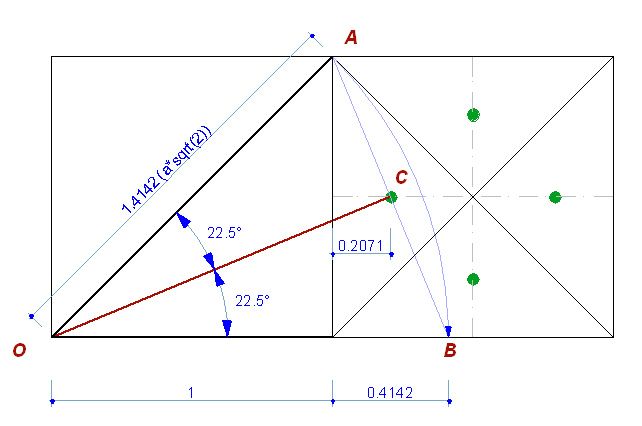
Рис. 8

Именно деление угла на равные части используется при построении 16 лучей. Образуется угол правильного восьмиугольника, а в основе звезды лежит не правильный, “ортогональный” восьмиугольник. Это противоречит логике ортогонального модульного построения общей композиции, но проецирует ту же логику (деление на 2) на радиальную систему. Таким образом, в композицию добавляется полярная система.

Обнаруживается конфликт (в противопоставлении) двух различных геометрических систем : правильной восьмиугольной звезды, построенной по принципам полярной системы, и “неправильной”, построенной на ортогональной модульной основе.

Этот конфликт заставляет систему модифицировать структуру внутренних связей, в стремлении к равновесию.

А вот для чего тогда остальные три точки?

Формируя собой диагонально повернутый квадрат, они показывают, что точки лежат именно на серединных осях ячейки, а не где-то ближе или дальше к вершине. И диагональные перекрестия ячеек, тоже помогают воспринять неточный рисунок правильно.

То есть, маркировка в (этом случае) нанесена для того, чтобы указать на то, что именно угол делится пополам лучами, а не сторона ячейки, как можно было бы, следуя логике общей композиции, предположить.

В противном случае, построив биссектрисы достаточно было бы остановить луч на стороне квадрата, в крайнем случае, довести до первой точки. Но нам даются именно все четыре точки, которые ассоциативно связывается в квадрат и с его помощью хорошо прочитываются правила построения.

Маркировочные точки, получается, нанесены не случайно, и не из эстетических соображений, а как уточнение чертежа, дающее гарантию прочесть чертеж правильно.

Почти одинаковая величина углов, получаемых в разных вариантах, может внести ошибку при прочтении, и, с расчетом того, что изменение логики построения может оказаться не замеченным, на этом моменте акцентируется внимание. Точки активно показывают, подчеркивают, что именно правила “правильной восьмиконечной звезды” работают в этой части чертежа. А это говорит о том, что чертеж обладает свойствами иллюстрации, т.е. он нарисован с учетом того что его будут читать. Маркировка, как семантические элементы, используется в качестве пояснений к чертежу, но для кого предназначены эти пояснения? И почему так важно одинаковые там углы или нет? Единственной ли является “проблема построения лучей”, или чертеж содержит гораздо больше информации?

Выводы об иллюстративном, указательном характере маркировки подтверждаются и следующим.

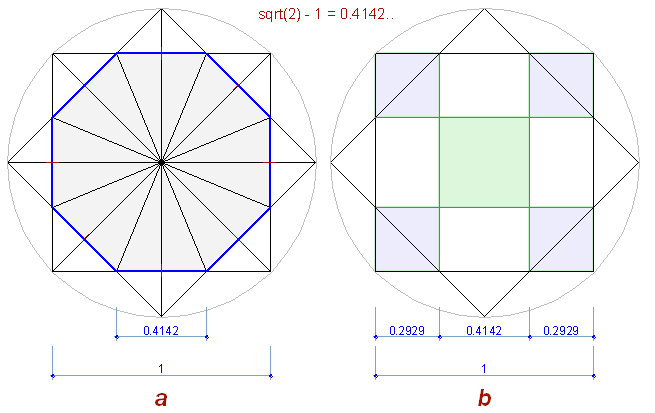
Рис. 9

При пересечении, два повернутых квадрата образуют правильный восьмиугольник (Рис. 9.a), со стороной равной sqrt(2) – 1 (при стороне квадрата = 1). Правильный восьмиугольник основан на пропорциональных отношениях стороны квадрата к его гипотенузе, выражающееся через корень квадратный из 2. И деление квадрата (Рис. 9.b) вершинами восьмиугольника происходит тоже с таким же пропорциональным коэффициентом, на иррациональные части.

Повернув этот рисунок (Рис. 9.b) на 45°, увидим, что это и есть маркировочные квадраты, обозначенные точками на геоглифе:

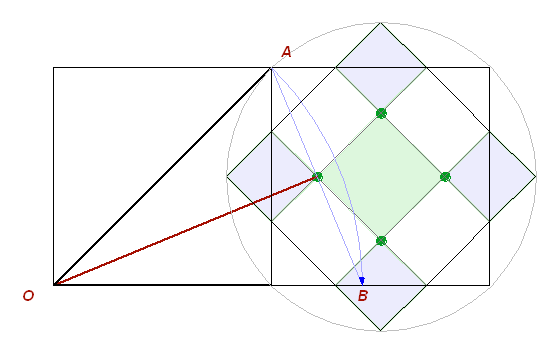
Рис. 10

Точки геоглифа в ячейках соответствуют иррациональным ячейкам квадрата правильного восьмиугольника.

Остается догадаться – где используются меньшие (синие) квадраты?.

20 из 64-х ячеек основного квадрата “замаркированы”.

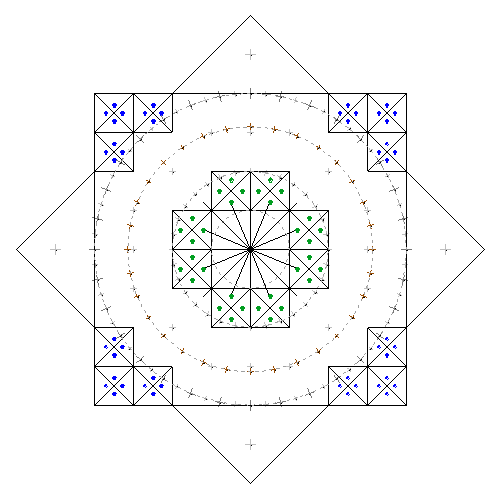
Рис. 11

На снимках геоглифа хорошо заметно, что размеры маркировочных квадратов различаются. Ячейки основного квадрата, расположенные в углах (12 шт.), маркируются явно меньшими по размеру квадратиками (я обозначил их синими точками), чем ячейки расположенные вблизи центра (8 шт. – зеленые точки). (Основной квадрат 8х8, а диагональ повернутого квадрата – 12)

Назовем их для удобства Qа – больший, и Qb – меньший:

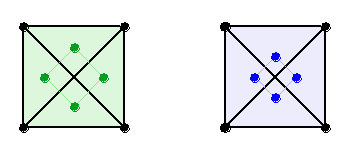
Рис. 12

Таким образом ячейки делятся на четыре типа: сначала на пустые и замаркированные, затем замаркированные большим квадратом Qа и малым Qb.

Если мы наложим пропорциональную матрицу, полученную на Рис. 9.b то заметим, что схема маркировки ячеек Qа и Qb квадратами совпадает с расположением соответствующих квадратов матрицы:

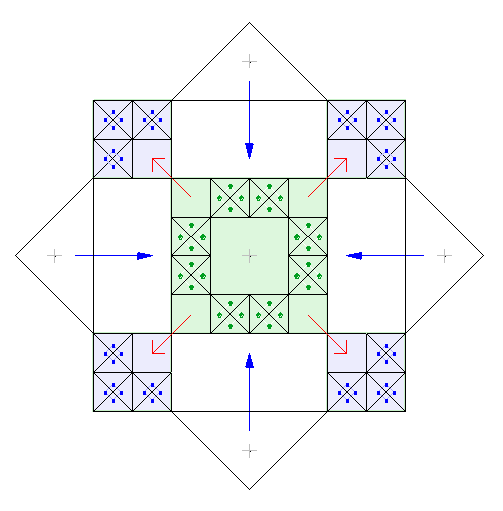
Рис. 13

В неправильной звезде пропорции матрицы адаптируются к модульным отношениям:

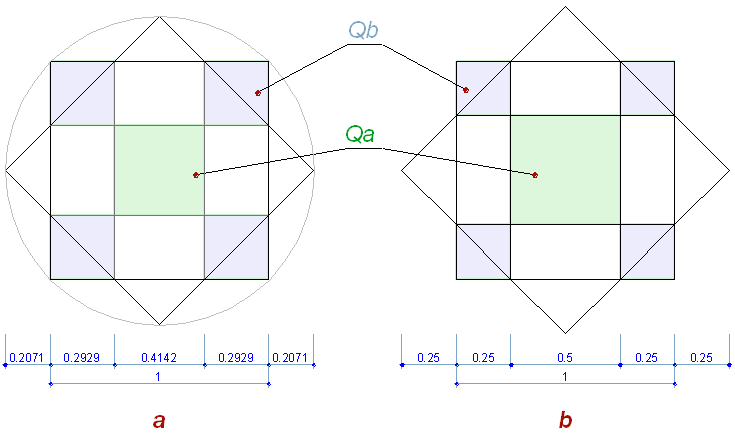
Рис. 14

И так мы видим, что матрица Qa-Qb квадратов (Рис. 14), включена в композицию как система пропорциональных отношений правильного восьмиугольника для построения 16-ти лучей, и выступает еще в качестве схемы маркировки ячеек, связывая прямоугольную и полярную систему. Расположение замаркированных ячеек еще раз подводит нас к тому, речь идет об отношениях полярной и ортогональной системы.

Что получается? Из центра звезды берет начало геометрия радиальной системы, а в результате нарисована прямоугольная звезда, подчиненная правилам ортогональной модульности.

Нарисовать уточек в углах, а по середине лодочку – это еще можно понять. Но рисовать квадратик со стороной относящейся к стороне ячейки в пропорциях построения радиальной системы и наслаждаться радостью того, как он выглядит, распределяя его по кругу в прямоугольной системе в виде замысловатых точек – это уже сложнее отнести к развлечению.

Получается, что расположение помеченных ячеек, размеры маркировочных квадратов являются явно демонстрируемыми признаками включения в общую композицию, построенную на модульной ортогональной основе, элементов радиальной системы правильной восьмиконечной звезды. Намекают на близость этих систем и на отличия, которые в корне меняют внутренние свойства композиции. Наличие таких внутренних связей между элементами, убеждает меня в том, что геоглиф носит информативный характер.

Технология элементов-подсказок, включенных в общую схему и так гармонично в ней работающих, исполняя функцию указательных знаков – не очень типична для традиционных методов изложения информации, берущих свое начало от математиков-философов древнего мира. Эстетическая составляющая является лишь канвой, основой для изложения информации, подобно игре слов в поэтическом изложении, несущей послойно уложенный глубинный смысл, явно не проявляющийся в конкретных словах. Л. Кэролу возможно доставляло удовольствие упаковывать математические измышления в забавные стихотворения для маленькой девочки. Но он имел образование соответствующее.

Каждый включаемый элемент в композицию, является значимым носителем некоторой информации, своего рода символом некоторого геометрического языка.

И мы рассмотрели только иллюстративный, демонстрационный характер композиции.

Продолжение следует…

Валерий Куликов

Источник

Еще по теме