Ханджян О.А., Ханджян А.О. Система Книги Перемен

Введение

“Все люди от природы стремятся к знанию. А наиболее достойны познания первоначала и причины, ибо через них и на их основе познается все остальное, а не они через то, что им подчинено.” Этими словами открывает свои сочинения Аристотель [1]. Там же убедительно показано, что исходным пунктом познания самого общего в природе, начал природы является их определение с помощью понятий, противоположных друг другу по смыслу. Таким образом, еще в глубокой древности было установлено, что язык противоположностей является универсальным языком описания начал природы.

Однако еще раньше, в истории человечества этот способ был интуитивно применен на практике. При этом история обозначила два противоположных подхода на этом пути. Первый подход связан с европейской цивилизацией, где за основу были взяты полярные (уничтожающие друг друга при взаимодействии) противоположности. Второй подход был принят и получил развитие на Востоке, где за основу были взяты противоположности дополняющие друг друга при определении целого.

Начала, которые были сформулированы таким способом, отвечают принципу дополнительности. Сравнительно недавно все это получило подтверждение в математике в теории полугрупп, где было показано, что эти два подхода являются, с одной стороны, единственно возможными и, с другой стороны, полностью самостоятельными [4].

Под влиянием этого выбора в истории сложились две культуры, две философии, две системы представления природы. То, что известно как европейская система, мы обсуждать не будем. Нас будет интересовать система представления, развитая на Востоке. Изложение этой системы в наиболее полном и законченном виде осуществлено в китайской Книге Перемен, аккумулировавшей труд многих поколений в прошлом по созданию и отработке этой системы [2,3].

Общая характеристика системы Книги Перемен

Напомним, что в Книге Перемен природа первоначально обозначена как целое и названа Великим Пределом. Исходным пунктом здесь является деление Великого Предела на два дополняющих друг друга понятия инь и ян. Далее этот простой принцип противопоставления дополняющих друг друга понятий развивается до универсальной системы представления реальности.

Делается это следующим образом. Путем последовательного дробления образуют более мелкие дополняющие друг друга части, что приводит к восьми символам – триграммам, затем эти символы размещают друг над другом попарно, что позволяет получить шестьдесят четыре гексаграммы. Гексаграммы это самостоятельные и независимые сущности, им приписано определенное обобщенное содержание причем так, что они полностью покрывают окружающую реальность. Тем самым создана система, в которой каждая гексаграмма в реальной ситуации соответствует событию. Реальность в этой системе определена через множество состояний, участвующих в непрерывном процессе преобразования к новым состояниям, т. е. определена как поток перемен или поток событий.

Такая система как модель воспроизводит хорошо наблюдаемые в природе причинно – следственные связи, взаимодействия в природе, в результате которых одно событие через определенное время вызывает другое событие. Если попытаться отметить наиболее общие свойства этой модели, то эта модель является асимметричной и ориентирована на свойство направленности времени, т. е. по своей сути является качественной моделью. Стрела времени играет здесь ведущую роль. Время в этой системе необратимо. Но, пожалуй, главное, что отображено в модели, это существующие повсеместно в природе циклы перемен. Другое важное свойство, которое отображено в модели, это принципиально вероятностный характер перехода от одного состояния к другому.

Однако в настоящее время многие свойства модели все еще вне досягаемости. Нет понимания в главном: не прослежена связь гексаграмм. Объясняется это тем, что, несмотря на многочисленные попытки, до сих пор не удалось понять устройство этой системы. Данная работа преследует именно эту цель и сегодня это уже можно безусловно сделать, опираясь на теорию временеподобных систем, развитую в [4].

Система Книги Перемен как временеподобная система

По совокупности перечисленных выше свойств система Книги Перемен это не более и не менее чем древнейший пример временеподобной системы. Для этого утверждения есть несколько оснований, но главное из них то, что в системе применено асимметричное начало, когда целое предшествует части, общее – частному.

Для гексаграмм в системе введены отношения упорядочения, отражающие динамику противоположностей, что также согласуется с теорией. Эти отношения определены в системе простейшим образом, как отношения соседства гексаграмм. Если пользоваться общепринятыми числами – номерами гексаграмм, то это можно записать как разбиение шестидесяти четырех гексаграмм на пары (1,2), (3,4),…. (63,64). Описанная выше структура (иерархия) гексаграмм и отношения гексаграмм это то, что образует костяк системы Книги Перемен, рассматриваемой как временеподобная система.

Движение и преобразование в процессе движения основа основ функционирования системы Книги Перемен. Применительно к ее структуре движение это взаимодействие и перемещение линий графических символов гексаграмм системы.

В теории временеподобного подхода используется логическая модель движения, которая определяет его как некоторый алгоритм [см. 4 п.5.3]. Этот алгоритм предполагает определение логическими средствами локальных максимумов и минимумов, связанных между собой по определенным правилам, что равносильно сортировке симплексов – абстрактных составляющих объекта движения. Этот алгоритм и будет применен для преобразования графических символов системы Книги Перемен. Оказывается, что с его помощью можно устранить неточности в имеющейся в нашем распоряжении информации по устройству системы, и определить потоки перемен, что дает ответ практически на все вопросы по устройству этой системы.

Сначала приведем алгоритм движения для случая триграмм, т.е. для случая пространства, квантованного на три уровня. Соответствующая схема приведена на рис.1.

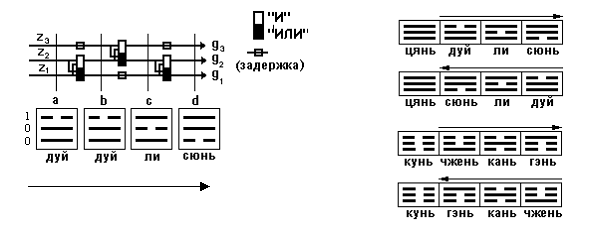
Рис. 1. Преобразование триграмм

Для удобства в схему введены задержки, позволяющие разделить выполнение алгоритма на условные этапы, следующие друг за другом. Считается, что величина задержки равна длительности преобразования в логических схемах. Для данной схемы имеем, следовательно, четыре этапа (от а до d) преобразования при движении от входа к выходу.

У триграммы, преобразование которой предполагается проследить, прерывные линии заменяются, например, единицами, а непрерывные- нулями. Будем называть этот способ кодирования основным. Если прерывные линии заменяются нулями, а непрерывные единицами, то это дополнительный способ кодирования. Теперь можно проследить по этапам, что происходит с триграммой при движении.

Процесс преобразования заключается в том, что анализируются пары линий триграммы, расположенные рядом, и, в зависимости от направления движения, либо все остается без изменения, либо линии меняются местами, если в паре находятся линии разного типа. При использовании основного способа кодирования прерывные линии последовательно продвигаются на более низкие уровни, а непрерывные на более высокие, при дополнительном – наоборот. Это приводит к тому, что в процессе преобразования возникает последовательность триграмм, следующих друг за другом.

Если триграмма составлена из линий одного типа, то она не изменяется при любом способе кодирования (триграммы цянь и кунь). Будем называть их базовыми. Триграммы чжень, гень, сюнь и дуй при одном из способов кодирования остаются без изменения, а при другом способе изменяются. Триграммы кань и ли во всех случаях трансформируются в другие триграммы.

Рассмотрим теперь квадратное расположение гексаграмм. Из первоисточников, дошедших до нас, известно три варианта такого расположения. Древнекитайские тексты свидетельствуют также, что этим исчерпывается их разнообразие. Это расположение по Фу-си, по Вэнь-вану и по мавандуйскому тексту, все они приведены в верхней части рис.2. Под ними в таких же квадратах показаны линии, соединяющие соседние гексаграммы из каждых двух, объединенных в пары по отношению порядка.

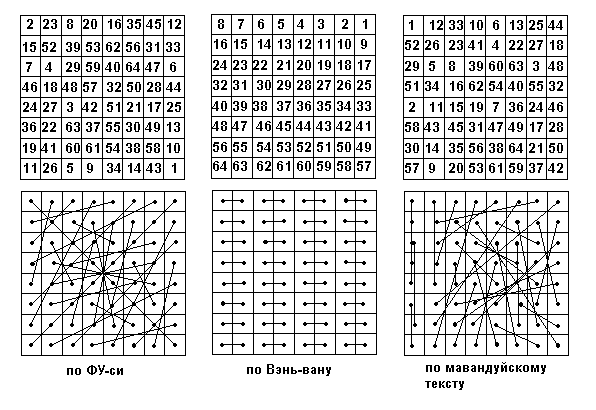
Рис. 2. Варианты расположения гексаграмм

Уже то, что существует несколько квадратных расположений гексаграмм, говорит о том, что создателей системы ни одно из них не удовлетворило полностью. Так в расположении по Фу-си обозначена иерархия гексаграмм путем полярного размещения по углам квадрата основных гексаграмм (гексаграммы 1 и 2, 11 и 12). В расположении по Фу-си есть определенная система в размещении пар гексаграмм, связанных отношением порядка. В ней просматривается диагональный крест, симметрия, но все же оно усложнено.

В расположении по Вэнь-вану достигается максимальное упрощение в изображении пар гексаграмм, связанных отношением порядка, но утеряна иерархия гексаграмм. В расположении по мавандуйскому тексту сделана попытка изобразить иерархию гексаграмм путем разделения квадрата на верхнюю и нижнюю половины, но не просматривается какая- либо система в расположении пар гексаграмм. Таким образом, только размещение по Фу-си является достаточно полным с точки зрения отражения свойств системы, однако, оказывается, что и в нем многое не учтено.

Итак, имеется две базовых триграммы: цянь и кунь. Будем использовать только основной способ кодирования. Возбуждение вносится в них путем замены одной из линий триграммы на противоположную линию. Тогда в рамках триграммы цянь наиболее неустойчивой (порождающей наиболее длинную последовательность триграмм при движении) будет триграмма дуй. Аналогичным образом, для триграммы кунь это будет триграмма чжень.

С учетом этого можно определить по две для каждой базовой триграммы, а всего четыре линейные последовательности триграмм, отличающиеся направлением распространения возбуждения, рис.1 (правая часть). На рисунке направление распространения возбуждения показано стрелкой, идущей от наиболее неустойчивой возбужденной триграммы к устойчивой возбужденной триграмме. Эта стрелка изображена непосредственно над линейной последовательностью.

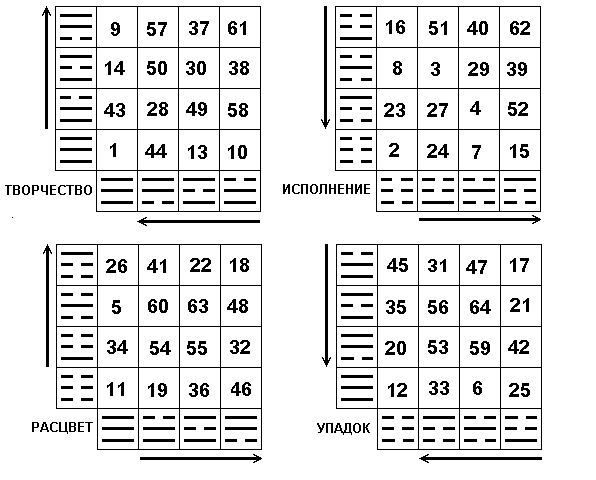
Рис. 3. Группы гексаграмм

Используем полученные линейные последовательности триграмм парами и без повторов для формирования гексаграмм. Линейную последовательность, триграммы которой применяются в качестве верхней триграммы гексаграммы, будем располагать вертикально, линейную последовательность, триграммы которой применяются в качестве нижней триграммы гексаграммы будем располагать горизонтально. Тогда имеем четыре группы по шестнадцать гексаграмм, показанные на рис.3.

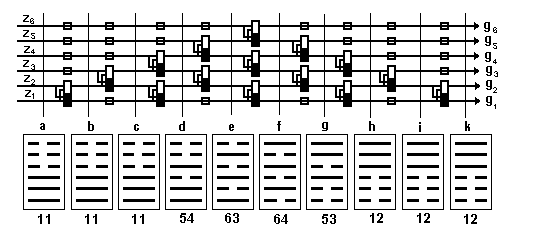
Рис. 4. Трансформация гексаграмм

Гексаграмма, образованная из базовых триграмм, дает название группе. Перечислим их: это творчество, это исполнение, это расцвет и это упадок. Каждая группа объединяет родственные по составу гексаграммы, а базовая гексаграмма группы – это ее своеобразный полюс. На рисунке показаны также стрелки направлений возбуждения. Хорошо видно, что это четыре взаимоисключающие друг друга варианта, созвучные названиям групп гексаграмм.

Рассмотрим гексаграммы групп с точки зрения их устойчивости и изменяемости при движении. Схема алгоритма движения для гексаграмм строится по тому же принципу, что и схема для триграмм, однако число уровней необходимо увеличить до шести. Будем считать, что для них возможны два вида движения: когда прерванная черта перемещается сверху вниз и когда прерванная черта перемещается снизу вверх (естественно, что сплошная черта перемещается при этом в противоположном направлении).

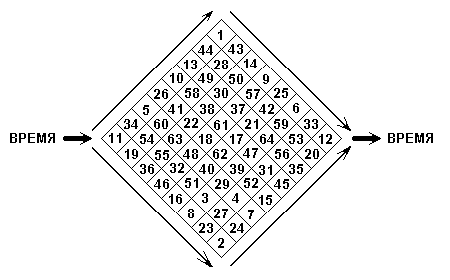
Рис. 5. Система гексаграмм (Модель Мира)

Это можно обеспечить по-разному, например, если применять то основной, то дополнительный способ кодирования, рис.4. Тогда получим, что базовые гексаграммы 1 и 2 как системообразующие не подвержены изменениям при любом направлении движения. Гексаграммы 43,44 и 23,24, базовая гексаграмма 11 и гексаграммы 34,19, а также базовая гексаграмма 12 и гексаграммы 20,33 не подвержены изменениям в одном из направлений движения и изменяются при другом. Это их важная особенность. Гексаграммы с указанным свойством как бы сосредоточены у полюсов групп. Все остальные гексаграммы групп изменяются как при одном, так и при другом направлении движения.

Полученные группы соединяются в систему. Порядок соединения определяется единым для всех групп процессом течения времени, задающего направления распространения возбуждения. Будем считать по европейской традиции, что течение времени происходит в направлении слева направо, тогда четыре группы гексаграмм Творчество, Исполнение, Расцвет, Упадок объединяются вместе как показано на рис.5.

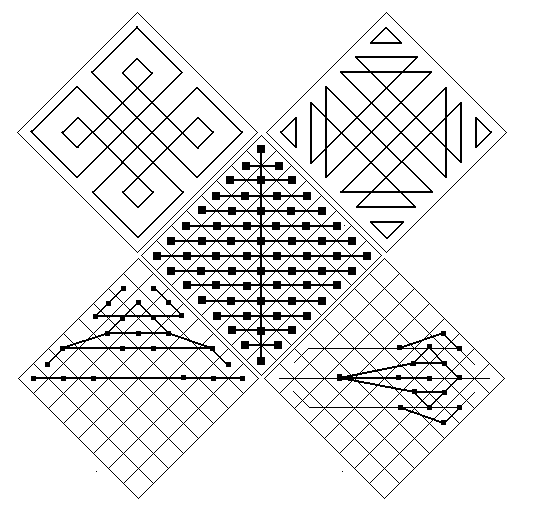
Рис. 6. Пары гексаграмм и траектории потоков перемен

Новое размещение является размещением с четырьмя полюсами: верхним – творчество, нижним – исполнение, левым – расцвет и правым – упадок. Схема линий, соединяющих гексаграммы, связанные отношением порядка, для новой системы приведена в центре рис.6.

Схема линий упорядочена в горизонтальном направлении времени, т.е. согласована с ним. Таким образом, в системе с новым квадратным размещением гексаграмм, наряду с показом иерархии, реализована упорядоченная по времени схема линий.

Зададимся целью как-нибудь более наглядно представить размещение пар гексаграмм, чем это достигается в схеме линий. Это можно сделать разными способами, но наиболее наглядным и простым оказывается способ на основе двух петлевых замкнутых кривых, показанных слева в верхней части рис.6. На этих кривых располагаются только те гексаграммы, которые являются парными друг к другу. Эта фигура интересна тем, что была, по-видимому, изобретена в те отдаленные времена, когда создавалась система “Книги Перемен”. Еще один способ показан в верхней части того же рисунка справа.

Другая принципиальная особенность нового размещения связана с возможностью наблюдения потока перемен. Прежде чем проследить это, напомним хотя бы некоторые из известных пояснений этого термина. “Ситуации, отраженные в “И цзин”, взяты непосредственно из жизни – это то, что случается со всеми изо дня в день и понятно всем, … вратами в систему может быть лишь простота и ясность. … Все мы от рождения находимся в едином потоке развития, но узнавание его и следование ему предполагает ответственность и свободный выбор” [3].

Итак, перемены бывают двух видов: естественные, связанные с природой вещей, обусловленные законами природы, и спонтанные, обусловленные выбором человека, но все же подчиняющиеся законам природы. Напомним, что в любом случае переход из одного состояния в другое совершается с некоторой вероятностью. В начале мы обсудим естественные перемены.

Используемый алгоритм (рис. 4) определяет все естественные потоки перемен. Для этого достаточно проследить с помощью алгоритма движения для каждой гексаграммы ее преобразование в другие гексаграммы при движении как в одном (основное кодирование), так и в другом (дополнительное кодирование) направлении движения. Имеем следующие две пары линейных последовательностей, общие для всех групп гексаграмм:

34-5-38-37-6-33 19-36-40-39-35-20

33-6-37-38-5-34 20-35-39-40-36-19.

Для групп гексаграмм “расцвет” и “упадок” имеем одну общую пару линейных последовательностей:

11-54-63-64-53-12

12-53-64-63-54-11.

Далее приведем отдельно по группам гексаграмм соответствующие линейные последовательности. Для группы гексаграмм “творчество” имеем:

61-37 30-57-6 28-50-57 44-13-10-9-14-43

61-38 30-58-5 28-49-58 43-14-9-10-13-44.

Для группы гексаграмм “исполнение” имеем:

62-39 29-52-35 27-4-52 23-8-16-15-7-24

62-40 29-51-36 27-3-51 24-7-15-16-8-23.

Для группы гексаграмм “расцвет” получим следующие линейные последовательности:

18-64 22-64 48-64 41-22 32-48 26-38 46-40

18-63 22-60-54 48-55-54 41-60 32-55 26-5 46-36.

И, наконец, для группы гексаграмм “упадок” получим:

17-64 21-59-53 47-56-53 42-59 31-56 25-6 45-35

17-63 21-63 47-63 42-21 31-47 25-37 45-39.

Последовательности гексаграмм показаны парами. Верхняя последовательность формируется при движении слева направо (основное кодирование), а нижняя при движении в обратном (дополнительное кодирование) направлении.

Естественные потоки перемен образуют своеобразные, но простые траектории движения. В большинстве случаев это циклы перемен, но не всегда. Для циклов перемен существуют две противоположные точки, которые задают пределы. Точки пределов это гексаграммы около полюсов, рассмотренные выше (рис. 3). Некоторые из траекторий показаны на рис.6 в его нижней части. Слева показаны частично траектории общие для всех групп гексаграмм и траектории для группы гексаграмм “творчество”. Справа – траектории для группы гексаграмм “упадок”. Анализ показывает, что для траекторий существуют диагональные симметрии как относительно вертикальной, так и относительно горизонтальной диагонали. Линейные последовательности, расположенные симметрично, образуют пару родственных линейных последовательностей.

Что касается спонтанных перемен, то они, скорее всего, хаотичны, имеют смысл перескоков с одной траектории на другую и должны совершаться более редко. Спонтанные перемены составляют, безусловно, важную часть формирования потока перемен, так как, например, к гексаграммам 61, 26 или 42 вообще можно перейти только этим способом.

Возникает естественный вопрос: “Не является ли это новым прочтением системы, искажающим первоначальный смысл и насколько адекватно новое квадратное размещение тому, что уже известно о системе Книги Перемен?” Нет, не является и, в тоже время, оно более адекватно системе, чем известные квадратные размещения.

Приведем пример. В разбиении шестидесяти четырех гексаграмм на пары выберем, например, нечетные гексаграммы и будем переворачивать их графическое изображение. Оказывается, что такое преобразование переводит графическое изображение нечетной гексаграммы в графическое изображение четной гексаграммы, которая является парой к первой. Таким образом, гексаграммы в паре являются перевернутыми по отношению друг к другу.

Исключение из этого правила составляют пары гексаграмм с номерами (1,2), (27,28), (29,30), (61,62). Здесь при переворачивании выбранная гексаграмма переходит сама в себя. Этот факт не имел объяснения. Теперь же он предельно ясен. Переворачивание с точки зрения квадратного размещения на рис. 5, есть движение в горизонтальном направлении (например, 13->14, 10->9 и т.д.). Гексаграммы, составляющие исключение, расположены по вертикали нового квадратного размещения и являются по переворачиванию, т. е. по движению в горизонтальном направлении парами сами к себе.

В то же время в этих парах (1,2), (27,28), (29,30), (61,62) наблюдается другой способ связи, объединяющий их в вертикальном направлении. Чтобы перейти в паре от первой ко второй гексаграмме, надо провести инверсию линий, заменить сплошную линию на прерывную и наоборот. Таким образом, новое квадратное размещение не только соответствует графическим начертаниям гексаграмм, но и позволяет сформулировать закон преобразования графических изображений гексаграмм в парах (1,2), (27,28), (29,30), (61,62).

Рис. 7. Порядок использования триграмм в гексаграмме

Более того, в процессе формирования нового квадратного размещения, по существу, был найден и общий закон формирования графических изображений гексаграмм. Этот закон состоит в том, что вводится возбуждение в гексаграммы соседние с базовой, а затем оно начинает распространяться при переходе к следующим соседним гексаграммам в этом размещении, что позволяет определить их графическое начертание.

Еще один общий вопрос: “Было ли известно создателям системы Книги Перемен новое квадратное размещение?” Мы убеждены, что квадратное размещение гексаграмм изначально существовало именно в таком виде, но история озвучила не окончательный, а промежуточные варианты размещения.

Только очень простые и ясные идеи построения могли быть использованы создателями системы и новое квадратное размещение позволяет их увидеть. Снова вернемся к графическому изображению гексаграммы. Триграмма, которая вошла в состав гексаграммы, может находиться либо вверху, либо внизу графического изображения гексаграммы. Возьмем новое квадратное размещение, в котором, как и прежде, каждый подквадрат соответствует определенной гексаграмме, рис.7.

От каждой триграммы проведем линию через те подквадраты, где она применяется в графическом изображении соответствующей подквадрату гексаграммы. Будем проводить линию по нижней части подквадрата, если триграмма находится внизу графического изображения, и по верхней части, если триграмма находится вверху. В результате имеем исключительно простой порядок построения, показанный на рисунке, в котором регулярно низ и верх меняются местами и строго выдерживается симметрия.

Система Книги Перемен как модель природы

Значение системы Книги Перемен выходит далеко за рамки гадательной системы. Вслед за ньютоновской моделью, это вторая глобальная модель природы. Вторая модель отражает действие разнесенных во времени причинно – следственных связей в природе, обусловленных ее асимметрией. Природа в этой модели предстает как ансамбль процессов непрерывного, непрекращающегося преобразования, движения от одних состояний к другим состояниям.

Эта модель показывает, что в этом случае существование в природе подчиняется закону циклических изменений, независимо от того рассматривается ли отдельное событие или вся природа в целом. Встроенная во время, эта модель предполагает периодическое чередование процессов развития и упадка, т. е. периодическое повторение моментов рождения, расширения, сжатия и стягивания в точку сингулярности.

Современная наука усилиями квантовой теории и теории относительности только еще прокладывает путь к этой модели.

Заключение

Новая теория движения [4], примененная к системе Книги Перемен, позволила разобраться в ее устройстве.

Эта теория показала, что в ряду общечеловеческих ценностей Книга Перемен должна быть поставлена на одно из первых мест. Это означает также, что использование возможностей, заложенных в систему Книги Перемен, на практике, скорее всего, только начинается.

Практическое применение. – А также теперь ясно, что при гадании нужно применять не одну случайным образом полученную гексаграмму, а надо (и теперь можно) смотреть наиболее вероятный путь развития от текущей гексаграммы в будущее.

Ханджян О.А., Ханджян А.О.

Список литературы:

1.Аристотель. Сочинения. Том 1,3, М., 1976.
2.Щуцкий Ю.К. Китайская классическая “Книга Перемен”.-М.:1997.
3.Вильгельм Р., Вильгельм Г. Понимание “И цзин”.-М:1998.
4.Ханджян О. Начала и основы теории представления. М., 2000.

Источник

Еще по теме