Рампрасад Согал. История арабских (индийских) цифр. Ноль и десятичная система счисления

Предислоаие П.Олексенко: данный текст представляет собой адаптированный перевод статьи индийского автора Рампрасада Согала (Ramprasad Soghal), опубликованной в 2016 г. в блоге автора. Автор рассказывает интересные факты о развитии десятичной системы счисления и нуля в древней Индии.

* * *

Всем известна важность математики и той мудрости, которая из нее выросла. Математика и торговля начали развиваться после открытия нуля и десятичной системы счисления. Это то, что знают все. Но мало кто знает, что европейцы хитро сократили количество чисел до индийско-арабских цифр, которые мы используем сегодня.

Сейчас после долгих и бурных дискуссий в научном мире принято считать, что ноль и десятичная система счисления появились в Индии. Сегодня мир согласен с тем, что Индия является источником этой неоматематики. Но это только полуправда. Никто не рассказывает, как на самом деле эволюционировали эти цифры. Почему мы пишем 0, 1, 2, 3, 4, 6, 9 именно так, а не в какой-то другой форме.

Различные символы были найдены в Сирии и Египте, даже в китайском и японском языках есть странные символы. Но дизайн чисел выглядит просто, с минимальным количеством штрихов, и он не подвержен влиянию ни одного из этих известных древних символов. В чем причина такой исключительности и как их придумали наши предки?

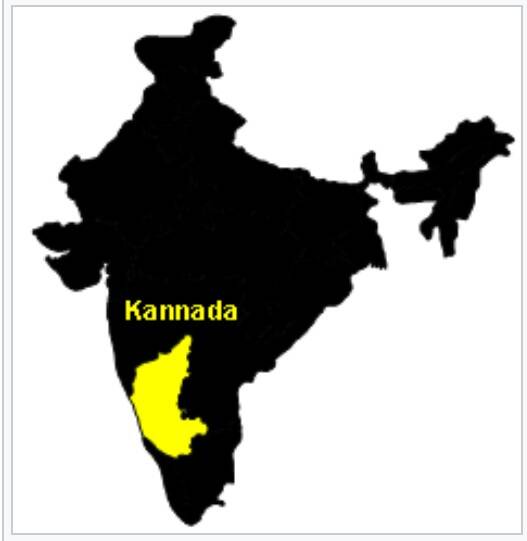
Географическое распространение языка ка́ннада. Это дравидийский язык, является одним из древнейших языков в Индии, распространён в юго-западной Индии, преимущественно в штате Карнатака. Родной язык представителей народа каннара и официальный язык индийского штата Карнатака.

В Индии история нуля и современных чисел началась в языке каннада. Поскольку только в языке каннада используются числа более или менее в первоначальном виде, то мы можем проследить полную историю чисел. Можно сказать, что, вероятно, числительные в том виде, в каком мы их знаем сегодня, были изобретены в Карнатаке.

Историкам остается только исследовать этот вопрос и доказать, что это правда. Однако, из-за разногласий в установлении дат тех или иных древних текстов, а также отсутствия письменных эпиграфических доказательств существования языка каннада до периода Ашоки, предоставить убедительное доказательство довольно сложно.

Слева: один из скальных храмов, справа: надпись на языке каннада 578 года (времен империи Чалукья) в пещерном храме № 3 в г. Бадами, который был королевской столицей династии Чалукья.

На языке каннада существует довольно интересная и странная книга – уникальное многоязычное литературное произведение под названием «Сири Бхувалайя» (सिरि भूवलय -“Siri Bhoovalay “).

Эту книгу написал джайнский монах Кумуденду Муни (Kumudendu Muni) ориентировочно в IX веке. Говорят, что в произведении около 600 000 стихов, что почти в 6 раз больше, чем в древнеиндийском эпосе «Махабхарата». Всего в ней 26 глав, составляющих большой том, из которых расшифрованы только три. Существует много споров о содержании, сложности, цели написания книги, дате написания и т. д. Однако прелесть этой книги в том, что она написана только цифрами.

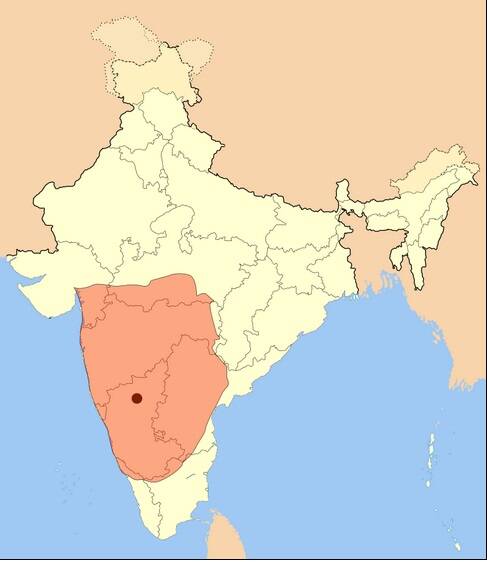
Империя династии Чалукья с VI по XII вв. Правление Чалукья ознаменовалось расцветом литературы на языке каннада и масштабным храмовым строительством.

То есть, язык книги — числа, и она называется «Анкха Кавья» (“Ankha Kavya”, что означает «Числовая поэзия»). Это, наверное, единственная книга в мире, написанная таким образом. В этой книге дается один формат написания – числа на языке каннада. В книге автор использует метрику поэзии каннада, различные шаблоны 18 основных языков и 700 малых языков/диалектов. На одной странице используются цифры от 1 до 64, расположенные в матрице 27×27.

По оценкам экспертов различные криптографические алгоритмы, используемые Муни Кумуденду, предназначались не для сокрытия содержимого, а для реализации текста на многих языках. Хотя книга написана на языке каннада, числовое произношение текста позволяет понять его людям, говорящим на других языках.

Пскольку ни один современный пандит (почётное звание учёного брахмана, а также человека высокообразованного в области классической индийской литературы на санскрите) не знаком с кодировкой, используемой в работе, специалисты работают над расшифровкой текста с помощью компьютерных программ.

Например, древние мудрецы, разбирающиеся в астрологии, уже видели изменение луны на небосклоне, новолуние и полнолуние. Сегодня, когда есть необходимость в разных расчетах, индийцы используют ведический лунный календарь Панчангам (पञ्चाङ्गम् , panchāngam).

Но как в древние времена люди могли записать новолуние или полнолуние, если числа еще не были придуманы? Новолуние означает отсутствие луны или ничего. Можно нарисовать горизонтальную линию, указывающую, что луны нет. А значок “О” может означать полнолуние. По мере роста луны можно писать кривые линии и увеличивать их количество до полнолуния.

Запись движения луны от дня безлуния до дня полнолуния, превратилось в систему счета. Такую десятичную систему (удобную при подсчете на пальцах) для записи чисел, генерируемых луной, мы можем видеть в древнем сценарии языка каннада.

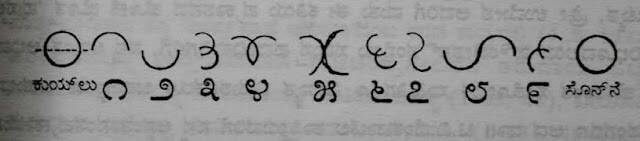
На фото показаны древний (вверху) и современный (внизу) способы написания чисел на языке каннада. По сути, особых отличий нет.

В тамильском языке, тоже относящемся к дравидийским языкам, эти коды уже другие.

Итак, безлунный день превратился в полный круг с перечеркнутой линией. Падья (первый день после новолуния) стал одним полукругом (точно так же, как это видно на небе). второй день превратился в две полукруглые линии, написанные одна над другой, что указывает на увеличение толщины. аналогично 3, 4 и т. д.

Обратите внимание, что 15-й счет превратился в полный круг, чтобы указать на полнолуние. Итак, древние математики установили схему счета до 15, которая является шестнадцатеричной системой, как мы знаем сегодня.

Полнолуние «О» представляло число 15. Знак «О» назывался «Пурна Анкха», то есть «полный знак, полное число» (полная луна на языке каннада – «Пурна чандра»). В древние времена с развитием торговли для транспортировки и хранения зерна, хлопка, масла и др. использовались большие мешки, а для ежедневного использования или обмена использовались глиняные горшки.

В итоге, когда шестнадцатеричная система была усечена до десятичной из-за удобства считать по пальцам, число 10 стало называться «Пурна Кумбха», то есть «полный горшок». И в наше время в сельской местности Карнатаки меряют традиционно, считая до 9 и далее на счет 10 говорят «Пурна Кумбха», и затем снова начинают процесс.

Древняя торговля и обмен подразумевали знание цифр и счета

Количество «Пурна Кумбха» становится значением для расчета платежа. Итак, «Пурна Анкха», то есть «О» стал использоваться для полного горшка «Пурна Кумбха» и таким образом символ полнолуния «О» был включен в число «10». Таким образом, в языке каннада можно объяснить причину происхождения всех цифр.

А далее индийские торговцы привезли эти цифры в Аравию, и те распространились повсюду. Поскольку опись вещей была трудоемкой, а большую часть письма составляли числа, простота символов каннада привлекла внимание всего мира, и они были приняты.

Впоследствии все большие числа были заменены. Эта система цифр в каннада была очень древней к тому времени, когда арабы достигли Европы. Нехватка полезных носителей для письма, отсутствие письма и копирования, а также необходимость соблюдения конфиденциальности в бизнесе изменили знаки чисел по целому ряду причин.

Самыми ранними формами письменности каннада являются надписи Маурьев в Индии. Историки зафиксировали, как выглядели цифры каннада в трудах династии Маурьев, и проследили их эволюцию до сегодняшнего дня.

В таблице показано, как числа менялись со времен Ашоки (III век до н.э.) и до наших дней (21 век) при разных правителях, правивших Карнатакой. Символы извлечены из опубликованных эпиграфических исследований. Внизу указана шкала времени, начиная с III века до н.э.

Написание полукруга один над другим все еще можно увидеть во времена Ашоки (первые три колонки в приведенной таблице). Обратите внимание, что Ашока использовал язык пали, а не каннада. Вероятно, к тому времени числа каннада уже были включены во многие языки Индостана.

Цифры и ноль в манускрипте Бакхшали

Манускрипт Бакхшали — древнеиндийская математическая рукопись, написанная на более чем 70 листах бересты (хотя, высушенные листьях пальмы заменяли бумагу в некоторых регионах Азии yже в XV веке до н. э.) и найденная в 1881 году в деревне Бакхшали недалеко от Пешавара (современный Пакистан). Она примечательна тем, что в ней есть точка, обозначающая ноль. Дата рукописи интриговала ученых в течение многих лет, и многие полагали, что она датируется IX веком, как и самый старый известный пример применения нуля в Индии, в индуистском храме Гвалиора, в индийском штате Мадхья-Прадеш. Теперь группа исследователей из Оксфордского университета и Бодлианских библиотек провела углеродную датировку рукописи и обнаружила, что она датируется периодом между вторым и четвертым веками!

Таким образом, манускрипт Бакхшали содержит самый старый зарегистрированный пример символа, который мы используем сегодня для обозначения нуля.

Древнейший символ нуля в виде точки на листе ╧ 16 рукописи из Бахшали, III-IV век. Фото: Bodleian Libraries, University of Oxford

А теперь давайте обратим внимание на то, что в рукописи Бакхшали ноль пока не фигурирует как самостоятельная цифра, а лишь как заполнитель в системе счисления. То есть в сценарии Бакхшали знак «О» указывает на наполнение «горшка» («кумбха»), например 10, 20, 30 и т. д.

Фигуры в древней надписи (предположительно V века), найденной в Бахшили (современный Пакистан). Ноль в манускрипте Бакхшали обозначен точкой

То есть знак «О» изначально не представлял собой число «ноль». Обычно цитируется ссылка на термин «шунья» в Упанишадах, чтобы доказать, что индийцы изобрели «ноль». Но это не совсем так. Действительно, «шунья» (शून्य – буквально – “ничего”) и «ананта» (अनन्त – буквально – бесконечный) были изобретены в Ведах, и они упоминаются, прежде всего, в Упанишадах. И шунья, и ананта были изобретены для описания Бога, чтобы указать, что все исходит от Создателя и все должно, наконец, слиться с Создателем. Это был аргумент, чтобы предложить: Слияние с творцом – это конечная истина, Жизнь – это возможность, и нужно использовать ее, чтобы достичь конечной цели за меньшее количество циклов рождения и смерти.

Ключ находится в Шастрах, которые представляют собой пояснительный текст к сутрам, каноническим текстам, или в более широком смысле – знание о каком-либо предмете или узкой области науки.

И здесь мы опять возвращаемся к языку каннада. Поскольку счет в каннада шел от 1 до «Пурна Кумбха» (полный горшок или полная луна), и термин «Пурна» (полный) был представлен знаком «О», а далее цикл повторялся, то начальная и конечная точка становятся одинаковыми, и соответственно, знак «О» стал обозначать начало и позднее был зафиксирован в некоторых культурах.

Перевод с языка каннада и английского языка Петра Олексенко

Оригинал статьи

См. еще: