Валерий Куликов. «Estrella» — Окружности и их периметры

Продолжение. Начало здесь.
Теперь попытаемся, используя обнаруженные ранее логические векторы и композиционные закономерности системы, подключить к «аппарату» оставшиеся элементы геоглифа — две группы концентрических окружностей, расположенных вне звезды. Правила геометрии звезды опять найдут подтверждение в интересных «совпадениях».
Сначала немного «правил».
Снаружи, рядом со звездой, изображены два «аномальных» объекта. На первый взгляд они не имеют со строгой геометрией звезды никакого отношения.
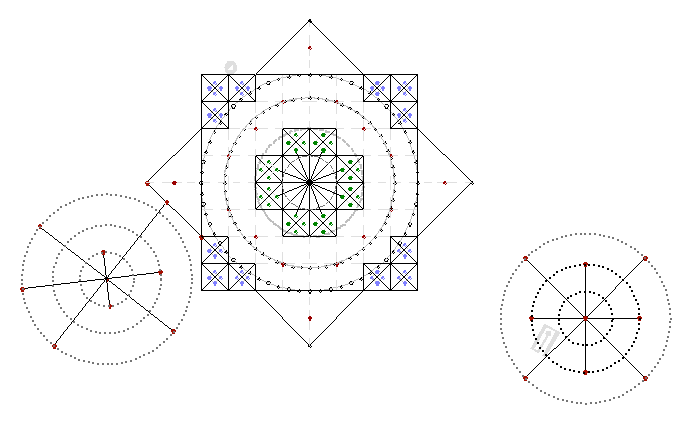
Рис. 1
Бросается в глаза, что окружности имеют те же радиусы, что и внутри звезды, и усажены на координатные оси.
В отличие от окружностей звезды, деления на них нерегулярные или не аккуратные, скорее даже не деления, а последовательность точек (ям) образующих окружность.
Кроме того, что это представители полярной системы, они по своему интересны с позиции геометрии:

*Третья окружность, как внутри звезды так и снаружи, при тщательном изучении фотоснимков, слегка больше окружности с радиусом 3. Поэтому предположил, что радиус равен пи. В дальнейшем я пока не заметил, на что это может повлиять, но так «интереснее» и больше похоже на сфотографированную действительность.
Почему опять пи? Это число является транслирующим коэффициентом между полярной и прямоугольной системой.
Разбиение окружности на количество сегментов, равное количеству делений на сторонах квадрата, также как и построение многоугольников с таким же числом сторон, наводит на мысль о том, что сегмент окружности ставится в соответствии делению стороны квадрата. Четверть дуги — сторона квадрата и т.д.
Таким образом окружность, развернутая в прямую, будет представлять из себя четыре длины квадрата соответствующего периметра или восьми сторонам восьмиугольника.
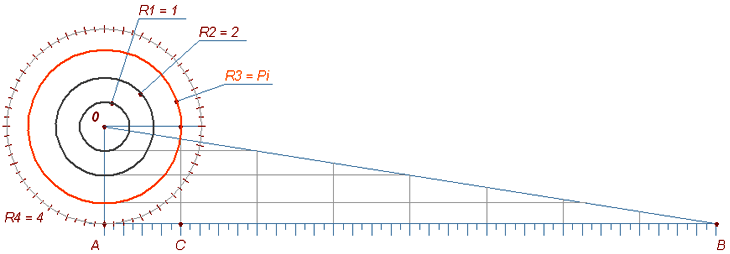
Рис. 2
На рис. 2 AB = 8 * пи = 25.1327412287183459077011470662360230735773551950008465677995567…
AC = пи = стороне восьмиугольника с тем же периметром или половина стороны квадрата (далеко не модульный квадрат).
Выстроенный же с помощью матрицы 64-угольник, с модульной стороной, в периметре почти равен описанной вокруг него окружности, радиус которой нам уже известен (Глава 3 рис. 5.). Для 64-угольника со стороной равной 1 этот радиус будет 10.19001.(длина окружности будет равна 64.02572, значение пи при этом — 3.14033). Точность не очень высокая, но если продолжать деление многоугольника, можно получить любую требуемую точность. Например, 2048-угольник дает радиус окружности 10.18592, периметр — 64.0003 и число пи при этом с точностью 5 десятичных знаков.
Отложив на рис. 24 от точки O вниз радиус (10.18592), а в длину выложим 64 модуля, получим:
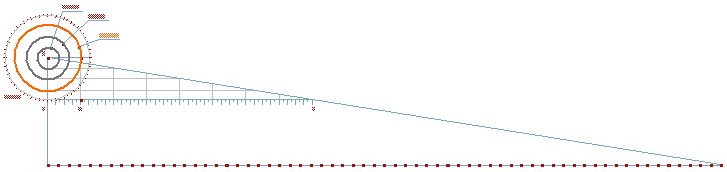
Рис. 3
Здесь величина сегмента 1/64 окружности равна модульной единице. Установлено соответствие угловой величины полярной системы с модульной единицей прямоугольной системы.
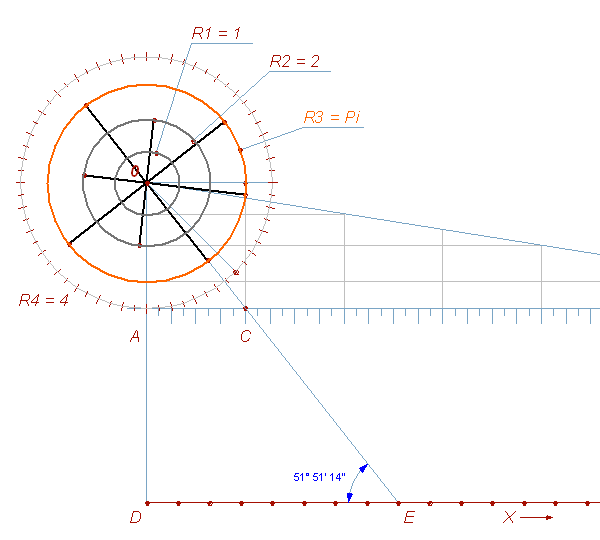
Рис. 4
Здесь DE равен 8 единицам, 1/8 от 64, стороне нашего квадрата или стороне матричного восьмиугольника на рис. 22.
С помощью этого «преобразователя» мы можем найти длину окружности нужного нам радиуса. По оси OD откладываем радиус и проводим до пересечения с OX. (где DX=64). И наоборот, мы можем получить радиус окружности с нужной нам длиной: отложим на DX длину, поднимем до пересечения с OX. Ордината этой точки и будет радиус.
Теперь — совпадения. Расположение окружностей вне звезды укладывается в эти правила!
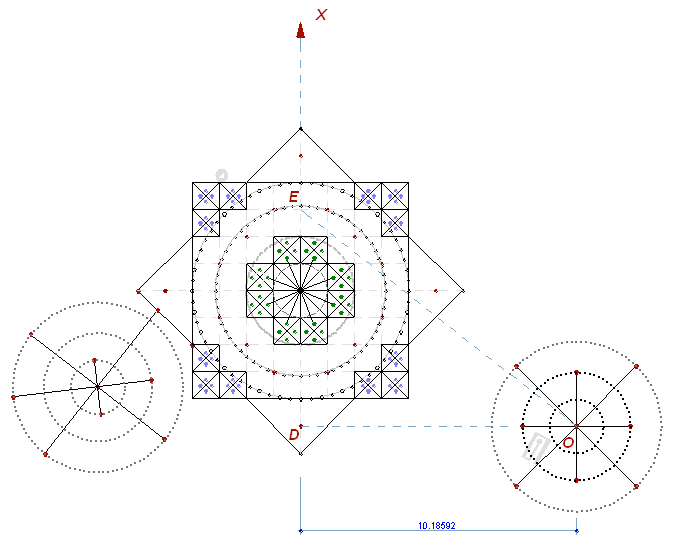
Рис. 5
Здесь только оси повернулись. OD = радиусу окружности с периметром 64, развернутым вдоль оси DX.
DE = 8.
Теперь, треугольник ODE повернем вокруг точки D и совместим O с вершиной, получив треугольник O’D’E’:
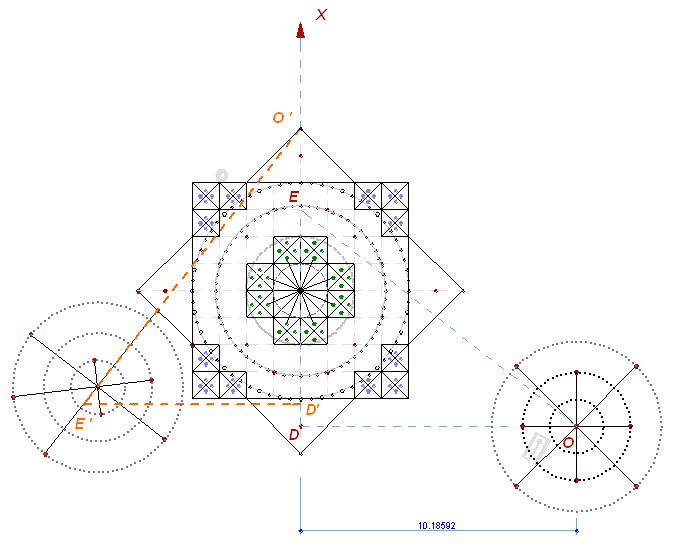
Рис. 6
Здесь, аналогично рис. 4, E’D’ = 8, или 1/8 часть периметра окружности с радиусом O’D’.
Левая группа окружностей фиксирует угол, который ставит в соответствие 1/8 длины окружности в основании (E’D’) и и ее радиус по высоте (O’D’).
Расположение окружностей по фотографиям трудно установить с точностью до 5-го знака, но смещение OD, и прохождение луча O’E’ я пытался проверить многократно, и о точность до десятых можно уверенно говорить (а это примерно толщина линии на геоглифе).
OD — порядка 10.2 — 10.3 модуля, — просматривается на снимках, сделанных с направлением камеры перпендикулярно этой линии. В этом случае, можно откладывать величину модуля, не опасаясь за перспективные искажения. Рельеф тоже в этом случае будет давать искажения вдоль оси Y, что не сильно повлияет на расстояние по оси X.
O’E’ — прохождение этого луча по клеткам геоглифа проверял подробно, а так же пересечение его с существующими и построенными характерными линиями.
Подробнее в приложении о точности чертежа.
Но нужна ли здесь точность? Ведь окружности не имеют на рисунке точной привязки. Величины на которые они указывают являются переменными, зависящими от стадии построения многоугольников. У 32-угольника это будет один радиус, а у 128-угольника — другой. Важно было указать, что «здесь находится радиус окружности, построенной на квадрате 16х16», а с какой точностью это будет сделано — дело техники.
Так же и с другой окружностью: она так же не имеет четкой привязки, что говорит о «плавающей» величине, зависящей от стадии развития системы. Но ось из точки E на геоглифе привязана к одной точке — она доводится до стороны диагонального квадрата и уверенно направляется на вершину звезды в точку O’. Такую «привязку» можно рассматривать как привязку вершины переменного угла E’O’D’. Эта ось является таким же переменным указателем как и линия OE на Рис. 4. Она может указать 1/8, или 1/4 периметра или весь периметр, меняя угол, но оставаясь в точке O. В данном случае этот луч указывает на угол отсекающий 1/8 периметра окружности, радиус которой указывают правые окружности.
Поэтому я уверен, что здесь, важна принципиальная схема:
Окружности в точке O указывают на радиус описанной окружности OD с периметром окружности 64.
Луч O’E’, отсекающий 1/8 длины окружности как сторону восьмиугольника или половину стороны квадрата с тем же периметром — очень характерно вписывается в общую логику. Угол (O’E’D’), получаемый в этом случае приближается к 51° 51’ 14”, в зависимости от точности нахождения радиуса OD.
Окружности, как и маркировочные точки, в этом случае, являются символами, отмечающими важные моменты композиции, намекая на пи и на связь данной части чертежа с полярной системой (окружности и их длина).
Окончание следует…
Валерий Куликов
Leave a reply
Для отправки комментария вам необходимо авторизоваться.



